
Das Verfahren der Mehrbildphotogrammetrie ermöglicht die genaue Bestimmung geometrischer Größen aus Bildern und hieraus die weitere Ableitung von 3D-CAD Modellen. Von dem aufzunehmenden Gebäude werden Fotos von unterschiedlichen Standpunkten aus mit beliebigen Aufnahmerichtungen ohne zusätzliche Messungen vor Ort gefertigt. Die Aufnahmerichtungen sollen untereinander konvergieren, die Standpunkte variieren. Am Gebäude selbst ist zur Maßstabsfestlegung mindestens eine Strecke zu bestimmen. Als Messkamera dient eine digitale Kamera, deren innere Parameter als hinreichend bekannt angenommen werden können. Anforderungen an eine Messkamera sind im PDF-Dokument "Image Aqcquisition for Digital Photogrammetry Using Off-The-Shelf and Metric Cameras " detailliert beschrieben.
Über korrespondierende Punkte in den Einzelbildern werden
durch die Auswertesoftware die Fotostandpunkte und die Koordinaten dieser Neu-
oder Orientierungspunkte berechnet. Da das System überbestimmt ist,
empfiehlt sich eine bestmögliche Anpassung aller Meßwerte durch eine
Ausgleichungsrechnung. Danach kann dann die Ausmessung der Details erfolgen.
Der Anwender hat zunächst Bildpunktmessungen durchzuführen,
danach wird die Bestimmung der Fotostandpunkte vorgenommen. Im Anschluß
daran erfolgt die Detailauswertung. Die ermittelten Meßdaten bilden die
Grundlage für die weitere CAD Modellierung
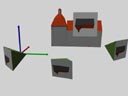 Bildverband / VRML
Bildverband / VRML1 Bildmessung
Aus den Pixelwerten der digitalen Bilder müssen die Bildkoordinaten korrespondierender Punkte ermittelt werden. Die gemessenen Pixel werden ggf. in das Fotokoordinatensystem transformiert. Wurde mit digitalen Kameras fotografiert, so stellen die Pixel bereits Fotokoordinaten dar. Hat man analoge Kameras benutzt und die Fotos gescannt, dann muss über Referenzmarken eine Transformation durchgeführt werden. In jedem Fall erfolgt eine Verbesserung der Photokoordinaten durch Berücksichtigung der Kameradaten. Das sind die Lage des Projektionszentrums und die Objektivverzeichnung. Details hierzu sind dem oben bereits genannten PDF-Dokument zu entnehmen.
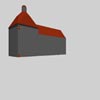
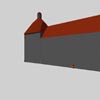
Eine simulierte Aufnahmesituation zeigt folgende Bilder mit den unterschiedlichen Aufnahmepositionen: Von links, aus der Mitte unten, aus der Mitte oben und von rechts.
 |
 |
 |
 |
Ein Klick auf den Link unter dem Übersichtsbild der
Aufnahmesituation (oben links) lädt die Kopnfiguration als VRML-Datei.
Informationen zu VRML finden Sie im Menüpunkt
Virtuelle
Realität. Dort können Sie auch einen VRML-Client
downloaden.
2 Modellbildung
2.1 Systemfestlegung
Am auszumessenden Objekt muß ein lokales Koordinatensystem
definiert werden. Hierzu bestimmt man insgesamt sieben Freiheitsgrade, drei
für die Translationen, drei für die Rotationen und einen für den
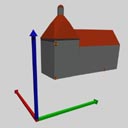
Maßstab. Im Bild links sind die drei Punkte zur Festlegung des Systems
markiert. Der untere rechte Punkt erhält per Definition Werte für X,
Y und Z. Dem oberen Punkt kann man den gleichen X- und Y-Wert zuordnen. Z
kennen wir hier nicht.Somit ist die blaue Achse (Z) definiert. Damit das
Koordinatensystem nicht mehr um Z rotieren kann, wird auf der rechten Seite der
Punkt mit Y festgelegt. Damit wären sechs Freiheitsgrade definiert. Wir
bezeichnen diese Minimalfestlegung mit 3-2-1 Definition. Als Maßstab kann
der Abstand zwischen den beiden unteren Punkten bestimmt sein oder eine
beliebige Strecke gemessen werden.
Punkte, die zur Festlegung des
Koordinatensystems dienen, sind bei der Bildpunktmessung korrespodierender
Punkte zu berücksichtigen. Anfangs- und Endpunkt der
Maßstabsfestlegung müssen ebenfalls zum Feld der korrespondierenden
Punkte gehören. Die Identifizierung der Punkte erfolgt über eine
Punktnummer, die Zugehörigkeit zu einem Foto über die Bezeichnung
bzw. Nummer des Fotos.
2.2 Photogrammetrisches Modell
Ein (photogrammetrisches) Modell liegt vor, wenn die relativen
Positionen zweier Bilder zueinander bekannt sind.
Jedes Bild hat einen
Standpunkt (X,Y,Z) sowie ein Aufnahmerichtung, eine Neigung und eine Kantung.
Kantung ist die Drehung um die Aufnahmeachse, die i.d.R. klein ist oder aber
zur Formatfüllung auch 45 grad betragen kann. Auch der Unterschied
zwischen "Portrait-Format" und "Landscape-Format" wird durch eine Kantung von
90 grad ausgedrückt.
Man definiert eine rechtes und ein linkes
Bild mit entsprechendem Abstand und konvergenter Aufnahmerichtungen. Der
Abstand wird als Basis bezeichnet. Die absolute Länge der Basis ist noch
nicht von Bedeutung. Bei der Modellbildung wird die relative Position des
rechten Bildes zum linken Bild ermittelt. Das sind fünf Parameter, drei
für die Rotation und zwei für die Translation. Von den
korrespondierenden Punkten, die man zur Berechnung benötigt (etwa 7 - 10)
sind im Anschluß an die iterative Bestimmung der Modellparameter die
Modellkoordinaten bekannt.
3 Bildorientierung
3.1 Kombinierte Rückwärtsschnitte und Vorwärtsschnitte
Über dem Punktfeld der Modellkoordinaten erfolgt jetzt die
Bestimmung von Standpunkt und Aufnahmerichtung des dritten Bildes. Das
Verfahren wird als räumlicher Rückwärtsschnitt bezeichnet.
Notwendig hierfür sind minimal drei Punkte des Modells. Eine erneute
Berechnung der Modellkoordinaten aus drei Bildern verbessert die
Punktgenauigkeit. Möglicherweise sind auch neue Punkte zu berechnen, die
in den Modellbildern bisher nur einmal zu identifizieren waren. Das Verfahren
der Berechnung eines Punktes aus zwei Bildern bezeichnet man mit
räumlichen Vorwärtsschnitt. Nach und nach werden durch dieses
iterative Verfahren Bilder neu in den Bildverband aufgenommen. Hierdurch
wächst auch die Punktwolkel der Modellpunkte.

3.2 Transformation auf die Systemfestlegung
Das gesamte Modell wird nunmehr auf die Systemfestlegung transformiert. Man überführt die Modellkoordinaten in Objektkoordinaten. Fehler in der Systemfestlegung können bisher nicht vorliegen, da mit der minimalen Festlegung von 7 Parametern gearbeitet wurde. Fehler in den Bildmessungen erkennt man an den Residuen. Das sind Abweichungen zwischen den ursprünglichen Messwerten und den in das Bild gerechneten Neupunkten.
Sofern man alle Fehler elimiert hat, können noch
weitere Messungen zur Systemfestlegung eingebracht werden. Die Berechnung wird
danach wiederholt. Sollten wiederum Fehler erkennbar sein, sind nur noch die
Messungen des Objektraums zu überprüfen.
3.3 Bündelausgleichung
Bei Anwendung eines Ausgleichungsprogramms erzielt man von der Orientierungsreihenfolge unabhängige Ergebnisse. Die Berechnungsergebnisse sind mit den Meßwerten (Beobachtungen) optimal abgestimmt (ausgeglichen). Daten gehen gewichtet in die Berechnung ein. Nivellierte Höhenunterschiede z.Bspl. mit Millimeter-Genauigkeit, gemessenen Koordinaten mit Zentimeter-Genauigkeit. Weiter liefert eine Ausgleichung Aussagen über die Genauigkeit und Zuverlässigkeit der Berechnungsergebnisse.
Das hier beschrieben Orientierungsverfahren wird von den verfügbaren Softwarepaketen in dieser oder ähnlicher Form angewandt. Der Anwender soll sich von dem komplexen Verfahren nicht abschrecken lassen. Im Anschluss an die Bildpunktmessung benötigt die Software zur Lösung der Gleichungssysteme nur wenige Augenblicke. Zur Interpretation der Ergebnisse liegen objektive Kriterien vor. Das sind u.a. der Gewichtseinheitsfehler der Bildpunktmessung nach der Ausgleichung, die Genauigkeit der Neupunkte und die Residuen der Bildmessung.
Detailkenntnisse der Algorithmen werden dem Anwender
nicht abverlangt. Das Wissen über den Berechnungsablauf ist aber zur
sachgerechten Verfahrensanwendung uind Ergebnisinterpretation notwendig.
Bereits bei Anlage der Bildverbände sollte die Auswertestrategie
berücksichtigt werden und auch schon die Detailauswertung vorausgeplant sein.
4 Detailauswertung
In den orientierten Bildern können nunmehr grafische Elemente gemessen werden. Das sind Punkte, Linien, offene und geschlossene Polygone im Raum oder in einer vorher bestimmten Ebene. Zur Definition einer Ebene müssen mindestens drei Punkte bekannt sein oder es können Projektionen auf das Koordinatensystem vorgenommen werden. Die Auswertung erfolgt in mehreren Bildern oder im Fall von ebenen Elementen aus nur einem Bild, den sog. Einbildmessungen. Zusätzlich zu den geometrischen Werten werden Attribute zur Selektion und Gestaltung der Grafikelemente mitgeführt. Zur Übersicht werden die Daten während der Auswertung jeweils in das digitale Bild eingeblendet.
Ein wertvolles Hilfsmittel bei der Auswertung stellt die Anzeige epipolarer Linien dar. Der Bestimmungsstrahl vom Bildpunkt durch das Projektionszentrum zum Objektpunkt eines Bildes wird in ein zweites Bild eingeblendet. Auf dieser Linie liegt dann auch der in diesem Bild noch zu messende Punkt und kein leichter identifiziert werden. Bei Hinzunahme weiterer Bilder werden entsprechend der bisherigen Messungen mehrere Epipolarlinien eingeblendet.
Entsprechend einer Tachymeteraufnahme werden alle relevanten Objektinformationen im photogrammetrischen Modell punktweise bestimmt. Die Rohdaten werden in einer CAD gerechten Datenstruktur gespeichert bzw. zur Weiterverarbeitung in ein Standardformat (DXF,X3D) konvertiert. Als weitere Anwendung der Mehrbildphotogrammetrie ist die Umbildung der Bilddaten von der perspektiven Abbildung in eine orthogonale Abbildung zu nennen. Die transformierten Rastererbilder sind dann als Texturen im geometrischen Modell zur photorealistischen Wiedergabe nutzbar.
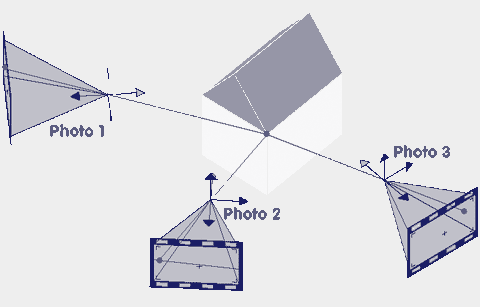
Abbildung: Punktweise Auswertung durch Mehrbildphotogrammetrie aus drei Bildern. Einblendung der Epipolarlinie in Photo 2